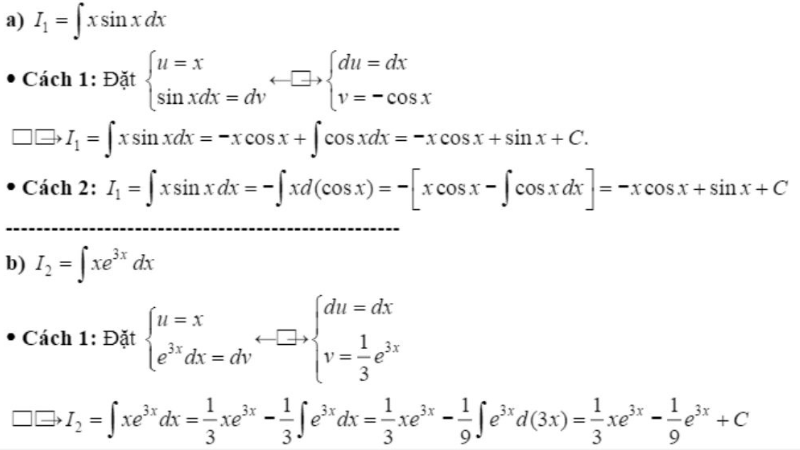Công thức nguyên hàm từng phần đã trở thành một công cụ quan trọng trong việc học toán học, đặc biệt là khi tiếp cận các khái niệm giải tích. Nắm vững công thức này sẽ giúp bạn tự tin hơn khi giải quyết bài tập, đặc biệt là nếu bạn đang chuẩn bị cho kỳ thi đại học hoặc muốn cải thiện khả năng tính toán của mình. Chúng tôi sẽ xem xét từng phần một một cách chi tiết trong bài viết này, kể từ định nghĩa và ví dụ thực tế.
1. Giới thiệu về công thức nguyên hàm từng phần
Công thức nguyên hàm từng phần là một công cụ toán học đơn giản và nó có thể được sử dụng trong nhiều lĩnh vực. Đây là một phần quan trọng của giải tích vì nó cho phép chúng ta giải quyết các bài toán phức tạp mà chúng ta không thể sử dụng các phương pháp tính nguyên hàm thông thường.
- Sự hiểu biết về các công thức nguyên hàm của từng phần không chỉ giúp bạn giải quyết nhanh các bài tập trong sách giáo khoa mà còn giúp bạn áp dụng chúng trong cuộc sống thực tế. Nhằm củng cố nền tảng kiến thức của bạn, chúng ta sẽ cùng tìm hiểu công thức này từ định nghĩa cơ bản đến các ứng dụng và bài tập vận dụng trong bài viết này.
Trong toán học, công thức nguyên hàm từng phần có ý nghĩa gì?
- Một trong những phương pháp hỗ trợ hữu ích nhất trong việc tính toán nguyên hàm là công thức nguyên hàm từng phần. Phân chia hàm số thành hai phần cho phép chúng tôi biến một bài toán khó thành một bài toán dễ hơn.
- Công thức này cũng giúp học sinh phát triển tư duy logic và khả năng phân tích vấn đề. Điều này rất quan trọng trong toán học và nhiều lĩnh vực khác, chẳng hạn như vật lý, kỹ thuật và kinh tế.
Lịch sử của công thức nguyên hàm của từng phần
- Các nhà toán học vĩ đại như Leibniz và Newton đã tạo ra các công thức nguyên hàm từng phần. Công thức này đã được cải thiện và hoàn thiện qua nhiều thế kỷ, trở thành một phần quan trọng của chương trình giảng dạy toán học hiện đại.
- Nghiên cứu nguồn gốc của công thức cũng nâng cao hiểu biết của chúng ta về sự phát triển của toán học. Điều này không chỉ cung cấp kiến thức mà còn thúc đẩy sự sáng tạo và phát triển trong lĩnh vực khoa học công nghệ hiện đại.
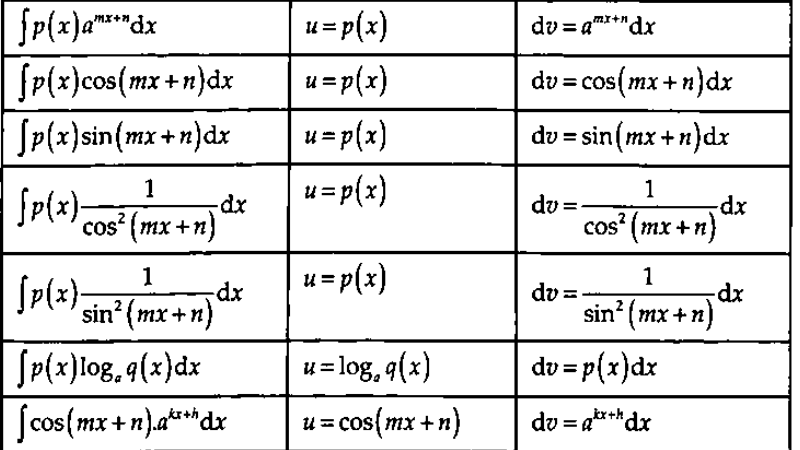
2. Công thức nguyên hàm từng phần trong toán học
Công thức nguyên hàm từng phần được tạo ra để tính toán các nguyên hàm phức tạp, đặc biệt là những hàm số có dạng tích của hai hàm khác nhau. Nó cho phép các nhà toán học giải quyết nhiều vấn đề giải tích.
Công thức như sau: [int u, dv = uv – int v, du ]
- Trong đó, các thành phần (u) và (dv) được chọn từ hàm cần có tính nguyên hàm. Để làm cho bài toán trở nên đơn giản hơn, rất quan trọng là phải chọn (u) và (dv) phù hợp.
Các thành phần trong mỗi phần của công thức nguyên hàm
- Ba thành phần chính là (u), (dv) và (du) trong công thức nguyên hàm từng phần. Kết quả cuối cùng có thể bị ảnh hưởng đáng kể bởi việc xác định đúng các yếu tố này.
- Chúng ta thường chọn một hàm có đạo hàm đơn giản hơn khi chọn (u). Đối với (dv), chúng tôi thường chọn phần còn lại của hàm mà chúng tôi có thể dễ dàng tính toán nguyên hàm. Cuối cùng, (du) là đạo hàm của (u), và (v) phải được tính cẩn thận từ (dv).
Các đặc điểm của công thức nguyên hàm của mỗi phần
- Từng phần có một số đặc điểm hấp dẫn trong công thức nguyên hàm. Một trong số đó là tuyến tính. Điều này có nghĩa là trong trường hợp có hai hàm số, nguyên hàm của tổng của cả hai hàm sẽ bằng nguyên hàm của mỗi hàm.
- Ngoài ra, công thức này cho phép áp dụng lặp đi lặp lại nếu cần thiết. Nếu bài toán chưa đơn giản hóa được sau khi áp dụng lần đầu tiên, chúng ta có thể tiếp tục áp dụng công thức với các thành phần mới cho đến khi bài toán trở nên đủ đơn giản để giải quyết.
3. Định nghĩa công thức nguyên hàm từng phần
Để hiểu rõ hơn về công thức nguyên hàm của từng phần, chúng ta phải tìm hiểu thêm về định nghĩa của chúng và cách chúng hoạt động. Công thức này chủ yếu được sử dụng để tính toán các nguyên hàm phi tuyến, trong đó hai hàm số được tích hợp để tạo ra một biểu thức phức tạp hơn.
- Điều này cho phép chúng tôi xác định các hàm số cần thiết để tách biệt và tính toán riêng biệt. Định nghĩa này không chỉ là lý thuyết mà còn có ứng dụng thực tế trong toán học hàng ngày.
Công thức nguyên hàm của mỗi thành phần được định nghĩa chi tiết.
- Một quy tắc giải tích cho phép tính toán nguyên hàm của một tích hai hàm số được gọi là công thức nguyên hàm từng phần. Chúng ta có thể giải quyết vấn đề một cách hiệu quả hơn bằng cách chia hàm số thành hai thành phần.
- Xác định (u) và (dv) là bước đầu tiên khi áp dụng công thức. Sau đó, chúng tôi tính toán (du) và (v) để đưa vào công thức. Tích của (u) và (v), cũng như nguyên hàm của (v) nhân với (du), sẽ được bao gồm trong kết quả cuối cùng.
Các ký hiệu trong công thức
- Các ký hiệu như (int), (du), (dv), (u) và (v) đều quan trọng trong công thức nguyên hàm của mỗi phần. Mặt khác, ký hiệu (int) biểu thị quá trình tính nguyên hàm, trong khi các hàm thay đổi (u) và (v) được biểu thị bằng các ký hiệu (du) và (dv).
- Các ký hiệu này không chỉ mang tính toán học mà còn cho chúng ta biết các thành phần trong công thức liên quan với nhau. Điều này giúp học sinh hiểu rõ hơn về cách các bài toán được tạo ra và cách giải quyết chúng một cách mạch lạc.
4. Bài tập vận dụng công thức nguyên hàm từng phần
Việc thực hành bài tập là rất quan trọng để củng cố kiến thức và kỹ năng ứng dụng công thức nguyên hàm từng phần. Bạn có thể áp dụng và luyện tập các bài tập mẫu sau đây.
Bài tập đầu tiên xem xét tính nguyên hàm của (x \cos(x))
- Hãy sử dụng công thức nguyên hàm từng phần để kiểm tra tính nguyên hàm của hàm s
ố (f(x) = x \cos(x). Để hoàn thành bài toán, hãy xác định (u) và (dv).
Bài tập thứ hai xem xét tính nguyên hàm của (e^x ln(x))
- Hãy sử dụng công thức nguyên hàm từng phần để thực hiện quy trình tính nguyên hàm với hàm số (f(x) = e^x ln(x). Để đạt được kết quả chính xác, hãy chọn các thành phần một cách hợp lý và theo dõi từng bước..
Bài tập 3 đề cập đến tính nguyên hàm của (sin(2x)ln(x))
- Tính toán nguyên hàm của hàm số (f(x) = sin(2x) ln(x) bằng cách sử dụng công thức nguyên hàm từng phần. Sao cho quá trình tính toán trở nên đơn giản hơn, hãy chú ý đến việc chọn lựa các thành phần.
Hướng dẫn giải bài tập
- Khi hoàn thành các bài tập, hãy nhớ kiểm tra kết quả của bạn bằng cách tính nguyên hàm của biểu thức mà bạn đã giải được. Điều này sẽ giúp bạn xác nhận kết quả là chính xác. Ngoài ra, đừng ngần ngại hỏi bạn bè hoặc giáo viên của bạn nếu bạn gặp khó khăn trong quá trình giải thích.
5. Tổng kết và lưu ý khi sử dụng công thức nguyên hàm từng phần
Trong toán học, công thức nguyên hàm từng phần là một công cụ rất hiệu quả, đặc biệt là khi tính toán các nguyên hàm phức tạp. Tuy nhiên, để sử dụng công thức này hiệu quả, một số điều cần lưu ý.
Lưu ý đến việc sử dụng (u) và (dv).
- Để đạt được kết quả mong muốn, các thành phần (u) và (dv) phải được chọn đúng cách. Hãy suy nghĩ kỹ lưỡng trước khi đưa ra quyết định và nếu cần, hãy thử nghiệm một số phương pháp để tìm ra phương pháp hiệu quả nhất.
Tìm hiểu kết quả.
- Hãy luôn kiểm tra lại kết quả của bạn sau khi giải quyết bài toán. Để thực hiện điều này, bạn có thể áp dụng lại đạo hàm hoặc sử dụng phần mềm tính toán để xác minh rằng nguyên hàm vừa tìm thấy là chính xác.
Thực hành hàng ngày
- Bạn cần thực hành thường xuyên để nắm vững công thức nguyên hàm của từng phần. Bạn sẽ cải thiện khả năng xử lý các bài toán phức tạp và làm quen với công thức nhờ điều này.
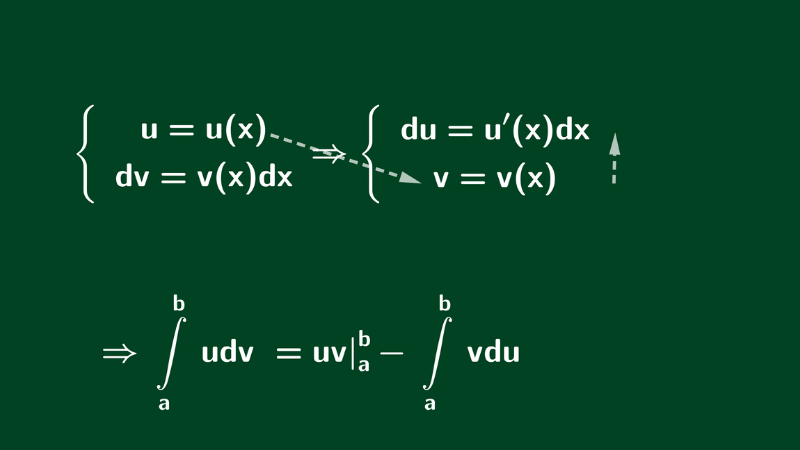
6. Kết quả
Chương trình học toán, đặc biệt là giải tích, không thể thiếu công thức nguyên hàm. Bạn không chỉ có thể giải quyết các bài toán trong sách vở mà còn có thể sử dụng các kỹ năng này trong thực tế.
Hy vọng rằng bài viết này đã cung cấp cho bạn bản tóm tắt và chi tiết về công thức nguyên hàm của từng phần. Hãy thực hiện những gì bạn đã học và không ngừng cải thiện khả năng toán học của mình. Chúc bạn thành công trong sự nghiệp học tập! Bạn cũng nên tìm hiểu thêm công thức logarit nó cũng rất quan trọng tròn toán học. Trên đây là bài viết về khám phá bảng công thức nguyên hàm, chi tiết xin liên hệ website: congthucnguyenham.com xin cảm ơn!